はじめに

編入試験の過去問の答えってないの?

大学のHPに掲載されていたり、大学に解答を請求すればもらえる大学もあるけど、すべての大学がそういう訳ではないね。
こんにちは。ななかぽ(@anadigian)です。
本記事では、2022年東京農工大3年次編入試験の過去問解答例をご紹介します。
農工大工学部は英語以外の過去問は公開しておりますが、模範解答の郵送や提示は行っていないようです。
参考になればよいかと思い、私の解答を公開することにしました。少しでも受験生のお役に立てれば幸いです。
解答例はすべての問題を網羅できていませんので、ご承知おきください。
問題自体は以下のリンクからご覧ください。
2020年も公開しました!
※物理はあまり得意ではないので掲載しておりません。
[2022年8月14日 追記]
この度、物理がお得意な方(@Dian_Qing_Wuさん)が物理と電気回路・電磁気学の過去問解答例のご提供を申し出てくださいました。
なので、物理と専門科目の問3(電気回路)と問5(電磁気学)を掲載いたしました。
@Dian_Qing_Wuさん、本当にありがとうございます!!
2022年 数学 解答例
クリック(タップ)で拡大できます。字が汚いのはご容赦ください。
※変数の宣言は省略しております。すみません。

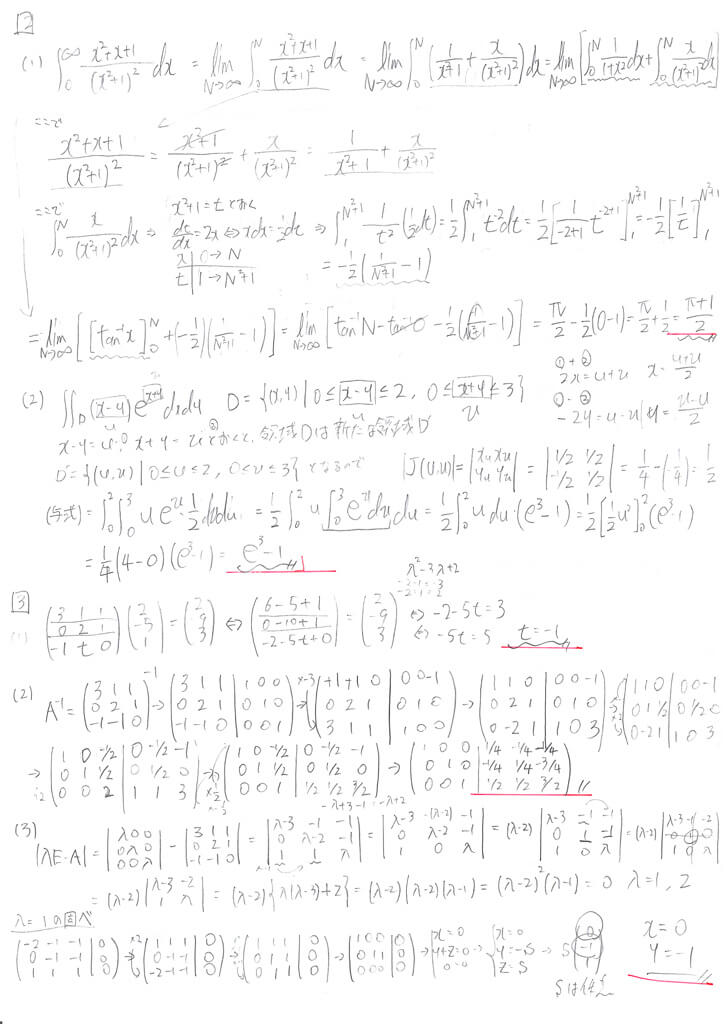

問1 極値問題
例年通りといった感じです。ヘッシアンが0にならないお利口な関数でした。
- 偏微分=0の式から停留点を求めます。
- 2階偏微分の式を用いてヘッシアンを求めます。
- そのヘッシアンの値で極値か否かを判定します。極値であるならば、$f_{xx}$の符号で極大か極小かを判定します。
$f_{xx}>0$なら極小値、$f_{xx}<0$なら極大値となります。
問2 広義積分と重積分
(1) 広義積分の問題です。この問題のミソは、この分数の形を積分ができる形に分解する点です。ここでは$\arctan$の積分と置換積分の和の形に持っていきます。
(2) 極座標変換でない$x+y$と$x-y$の2つを別の文字で変換して解く重積分の問題です。この与式の場合、置換する場所がはっきりとわかりますね。
問3 行列
2022年の行列の問題は易しめです。
(1) 行列の積を計算して$t$を求めるだけです。
(2) (1)の結果を用いて逆行列を求めるだけです。
(3) 固有値を求めて、最小の固有値に対する固有ベクトルを求めるだけです。
問4 微分方程式
2階線形微分方程式です。特解を$Ax+Be^{-x}$とするのではなく、$Ax+Be^{-x}+C$とするのがミソです。
2022年 物理 解答例 (提供)
クリック(タップ)で拡大できます。




問1 力学
野球のバットにボールがあたり、バットが回転運動する問題です。
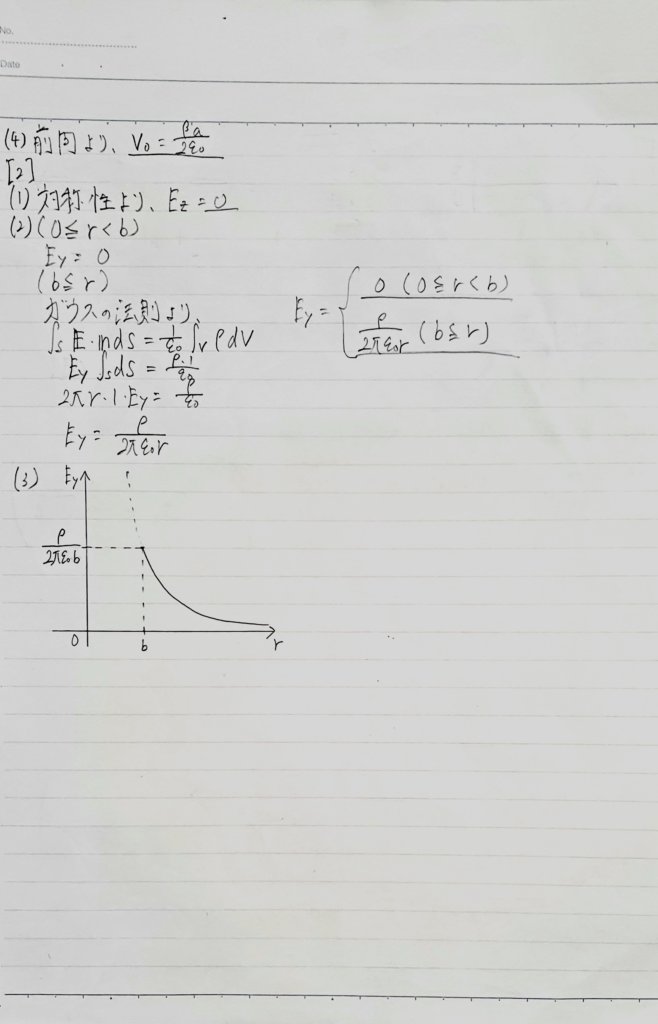
問2 電磁気学
一般的な電磁気学の問題です。
2022年 専門(知能情報システム工学科) 解答例
問1 計算機基礎
クリック(タップ)で拡大できます。

[1] 基数変換・固定小数点数
(1) 単なる基数変換の問題です。
(2) 固定小数点数の問題です。符号付き整数で負の数を求めるには反転して+1をすることにより、2の補数を求めます。
(3) 符号なし固定小数点数の問題です。
[2] 集合
集合の問題です。ベン図を書くことでそれぞれの数値がどの領域にあるのかを把握しましょう。
問題文で示されている「対称差」は「XOR」のことであり、「集合差」は「差集合」のことです。
[3] 確率
まず合計の玉の数と赤の玉の数が与えられているので、白の玉の数も必然的にわかります。よって、
箱I{赤4、白6}, 箱II{赤5、白5}, 箱III{赤6、白4}だとわかります。
(1) 赤の合計数が0のときの3つの箱からそれぞれ1つずつ取り出される色の組み合わせは{I,II,III}={白、白、白}、赤の合計数が1のときの色の組み合わせは{赤、白、白}・・・というように、まず赤の数による組み合わせを考えます。
{赤、白、白}と{赤、赤、白}の配置方法はそれぞれ3通りあることに注意します、
後は{白、白、白}、{赤、白、白}、{赤、赤、白}、{赤、赤、赤}のそれぞれについて、箱I,II,IIIから玉を1つずつとる確率を求め、積をとるだけです。
(2) 箱Iにのみ注目します。10個の中から3個の玉を同時に取り出すので、分母は共通して10C3となります。分子は取り出される赤の数(0~3)によって変わるのでそれぞれ計算します。
問2 論理回路
クリック(タップ)で拡大できます。

[1] 論理回路基礎
(1) 真理値表を問題文の通り書きます。
(2) (1)の真理値表に続きカルノー図を書きます。論理式は真理値表の出力が1の箇所に注目し、主加法標準形で記述します。
(3) (2)のカルノー図において、できるだけ大きく囲える$2^n$の塊で囲みます。その結果から簡単化された論理式が求められます。
[2] 同期式順序回路
(1) 指示通りに解きます。
(2) 状態遷移図の問題です。うまく書けなかったため割愛させていただきます。
問3 電気回路 (提供)
クリック(タップ)で拡大できます。


問4 ダイクストラ法
グラフ理論も出るようですね。今回は最短経路を求めるアルゴリズムである「ダイクストラ法」の問題です。そしてなんと、そのアルゴリズムは問題文に書かれております!
ダイクストラ法をご存知でない方は以下の動画が非常に参考になります。ぜひ見てみてください。
(1) 隣接行列の定義に沿って求めます。考え方として、この行列の左側(縦)と上側(横)にそれぞれ左上を$v_0$とし$v_1,v_2,・・・$と各々書き込みます。そして縦のノードから横のノードへの距離は××というようにして距離行列を作ります。
0 10 15 999 999 999 999 999 999
10 0 10 5 20 30 999 999 999
15 10 0 999 20 20 999 999 999
999 5 999 0 5 999 15 25 999
999 20 20 5 0 10 5 25 999
999 30 20 999 10 0 999 20 999
999 999 999 15 5 999 0 999 5
999 999 999 25 25 20 999 0 5
999 999 999 999 999 999 5 5 0例えば、上記の隣接行列の「30」は$v_1$(縦)から$v_5$(横)への距離は$30$ということになります。
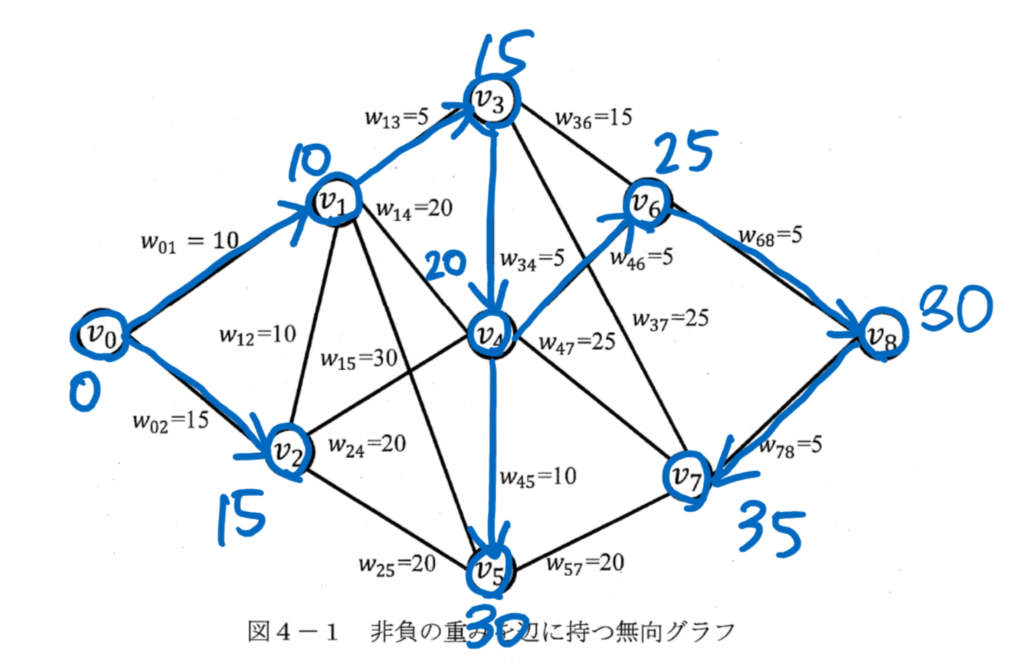
(2) ダイクストラ法のアルゴリズムは問題文中に記載されていますので、それを見ながら図で追っていきます。
$x$から$v_7$までの最短経路:$x(=v_0), v_1, v_3, v_4, v_6, v_8, v_7$
$x$から$v_7$までの最短距離:$35$
雑ですが、以下に経路を示します。
(3) ダイクストラ法のプログラムの穴埋めです。4か所の穴埋めがあるdo-while文の箇所を抜粋しております。
do
{
/* STEP-1 */
p = next, Q[p] = FALSE, min = INT_MAX;
/* STEP-2 */
for (i = 0; i < N; i++)
{
if (Q[i] == FALSE) continue;
if (W[p][i] < INT_MAX && d[p] + W[p][i] < d[i])
{
d[i] = d[p] + W[p][i]; // (1)の空欄
}
if (d[i] < min)
{
min = d[i], next = i; // (2)と(3)の空欄
}
}
} while (min != INT_MAX); // (4)の空欄問題では省略されていた、[1]で求めた隣接行列を配列W[N][N]に格納する関数setWは以下のように記載しました。
void setW(int W[][N])
{
FILE* fp;
fp = fopen("adjacency_matrix.txt", "r");
if (fp == NULL)
{
printf("file does not open\n");
exit(1);
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
fscanf(fp, "%d", &W[i][j]);
}
}
fclose(fp);
}実行結果は以下の通りです。
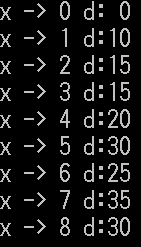
問5 電磁気学 (提供)
クリック(タップ)で拡大できます。







コメント