はじめに

編入試験の過去問の答えってないの?

ななかぽ
大学のHPに掲載されていたり、大学に解答を請求すればもらえる大学もあるけど、すべての大学がそういう訳ではないね。
こんにちは。ななかぽ(@anadigian)です。
本記事では、2020年東京農工大3年次編入試験の過去問解答例をご紹介します。
農工大工学部は英語以外の過去問は公開しておりますが、模範解答の郵送や提示は行っていないようです。
参考になればよいかと思い、私の解答を公開することにしました。少しでも受験生のお役に立てれば幸いです。
解答例はすべての問題を網羅できていませんので、ご承知おきください。
問題自体は以下のリンクからご覧ください。
2020年 数学 解答例
クリック(タップ)で拡大できます。字が汚いのはご容赦ください。


問1 極値問題
例年通りといった感じです。
- 偏微分=0の式から停留点を求めます。
- 2階偏微分の式を用いてヘッシアンを求めます。
- そのヘッシアンの値で極値か否かを判定します。極値であるならば、$f_{xx}$の符号で極大か極小かを判定します。
$f_{xx}>0$なら極小値、$f_{xx}<0$なら極大値となります。
問2 重積分
積分順序を変更して解く重積分の問題です。解析学の教科書の例題にも似たような問題があったような気がします。
問3 行列
行基本変形を用いて4つの未知数$a,b,c,d$を決定する問題です。
問4 微分方程式
2階線形微分方程式です。特解を$Ax^2e^{-3x}$として、Aを決定します。
2020年 物理 解答例
クリック(タップ)で拡大できます。



問1 力学
剛体振り子の問題です。
問2 電磁気学
電気影像法を使う問題です。
2020年 専門(情報工学科) 解答例
問1 情報理論
クリック(タップ)で拡大できます。
[2]や[4]は自信がないため、あまり参考にならないかもしれません...
問2 二分木
二分木に関する問題です。
[1] (1) いる (2) $O(log_2{N})$ (3) $O(N)$
[2]&[3] 二分探索木を通りがけ順序で走査するプログラムの穴埋め問題です。
#include <stdio.h>
#include <stdlib.h>
struct tnode
{
struct tnode* left; /* 左部分木へのポインタ */
int name; /* ノードの値 */
struct tnode* right; /* 右部分木へのポインタ */
};
struct tnode* gentree(struct tnode* p, int value)
{
if (p == NULL) {
p = (struct tnode*)malloc(sizeof(struct tnode));
p->name = value;
p->left = p->right = NULL;
}
else if (value < p->name) {
p->left = gentree(p->left, value); /* (4)の空欄 */
}
else {
p->right = gentree(p->right, value); /* (5)の空欄 */
}
return p;
};
void treewalk(struct tnode* q)
{
struct tnode* w[128]; /* w[]は最大128個の要素を保存できるスタック */
int sp = 0; /* スタックを管理する変数 */
while (!(sp == 0 && q == NULL)) {
while (q != NULL) { /* 葉に到達するまで左に進む */
w[sp++] = q; /* 親の位置をスタックに積む */
q = q->left;
// q = q->right;
}
sp--; /* spを親に移動する */ /* (6)の空欄 */
printf("%d\n", w[sp]->name);
q = w[sp]->right; /* 次の子ノードに移動し、ノードqに代入する */ /* (7)の空欄 */
// q = w[sp]->left; /* 次の子ノードに移動し、ノードqに代入する */
}
}
int main(void) {
struct tnode* root = NULL;
int i;
int data[12] = { 23,18,30,14,20,25,40,4,16,19,21,24 };
for (i = 0; i < 12; i++) {
root = gentree(root, data[i]);
}
treewalk(root);
return;
}実行結果は以下の通りです。
[4] 関数treewalk内の以下の箇所を変更します。
| 数値を昇順に表示 | 数値を降順に表示(変更後) | |
| 34行目 | q = q->left | q = q->right |
| 39行目 | q = w[sp]->right | q = w[sp]->left |
変更後の実行結果は以下の通りです。
問3 論理回路
クリック(タップ)で拡大できます。
問4 浮動小数点数
(タップ)で拡大できます。




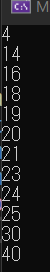
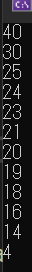




コメント